Transformations In Linear Regression

There are many reasons to transform data as part of a regression analysis.

to achieve linearity.
to achieve homogeneity of variance, that is, constant variance about the regression equation.
to achieve normality or, at least, symmetry about the regression equation.

A transformation that achieves one of these goals often ends up achieving all three. This sometimes happens because when data have a multivariate normal distribution, the linearity of the regression and homogeneity follow automatically. So anything that makes a set of data look multivariate normal in one respect often makes it look multivariate normal in other respects. However, it is not necessary that data follow a multivariate normal distribution for multiple linear regression to be valid. For standard tests and confidence intervals to be reliable, the responses should be close to normally distributed with constant variance about their predicted values. The values of the predictors need not be a random sample from any distribution. They may have any arbitrary joint distribution without affecting the validity of fitting regression models.

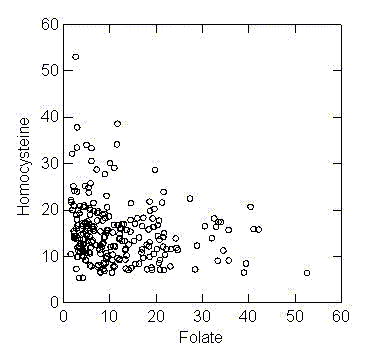Here are some data where the values of both variables were obtained by sampling. They are the homocysteine and folate (as measured by CLC) levels for a sample of individuals. Both variables are skewed to the right and the joint distribution does not have an elliptical shape. If a straight line was fitted to the data with HCY as a response, the variability about the line would be much greater for smaller values of folate and there is a suggestion that the drop in HCY with increasing vitamin status is greater at lower folate levels.

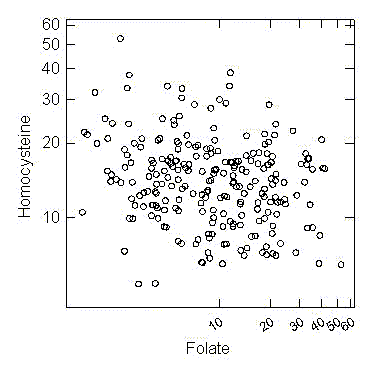When logarithmic transformations are applied to both variables, the distributions of the individual variables are less skewed and their joint distributions is roughly ellipsoidal. A straight line seem a like reasonable candidate for describing the association between the variables and the variances appear to be roughly constant about the line.

Often both variables will not need to be transformed and, even when two transformations are necessary, they may not be the same, When only one variable needs to be transformed in a simple linear regression, should it be the response or the predictor? Consider a data set showing a quadratic (parabolic) effect between Y and X. There are two ways to remove the nonlinearity by transforming the data. One is to square the predictor; the other is to take the square root of the response. The rule that is used to determine the approach is, "First, transform the Y variable to achieve homoscedasticity (constant variance). Then, transform the X variable to achieve linearity."

Transforming the X variable does little to change distribution of the data about the (possibly nonlinear) regression line. Transforming X is equivalent to cutting the joint distribution into vertical slices and changing the spacing of the slices. This doesn't do anything to the vertical locations of data within the slices. Transforming the Y variable not only changes the shape of regression line, but it alters the relative vertical spacing of the observations. Therefore, it has been suggested that the Y variable be transformed first to achieve constant variance around a possibly non-linear regression curve and then the X variable be transformed to make things linear.